Angle correction in XtalOpt

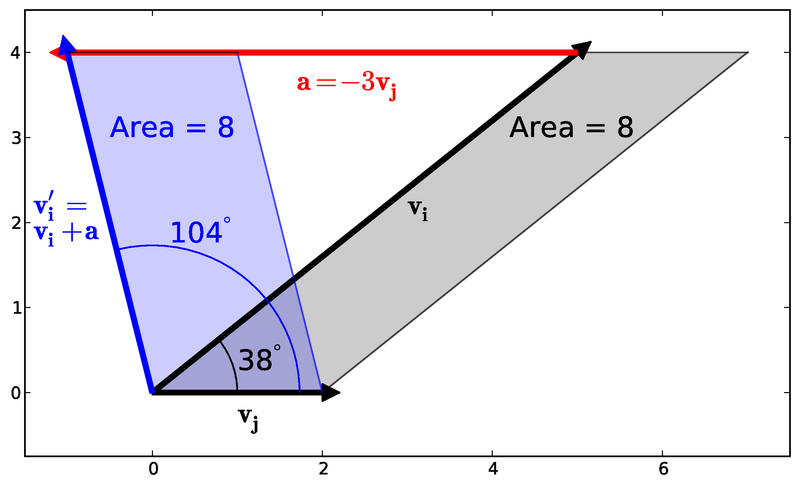
Example of the angle correction transformation in two dimensions

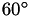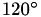Prior to optimization, the structure's lattice is adjusted so that all angles are between $60^\circ$ and $120^\circ$ ; by a process similar to that described by Oganov et al. in their 2008 paper. The following transformations are applied to all combinations of the three lattice vectors:

If both conditions

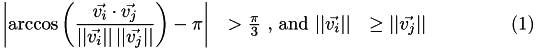
$\begin{eqnarray} \left| \arccos\left(\frac{\vec{v_i}\cdot \vec{v_j}} {||\vec{v_i}||\,||\vec{v_j}||} \right) - \pi \right| &> \frac{\pi}{3} \mbox{\ ,\ and\ } ||\vec{v_i}|| &\geq ||\vec{v_j}|| \end{eqnarray}$

are true, the cell should be transformed. To do this, the vector 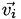$\vec{v_i}$ is replaced by the vector 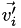$\vec{v_i'}$ , defined as

$\vec{v_i'} = \vec{v_i} - \mbox{ceil}\left(\left|\frac{\vec{v_i}\cdot \vec{v_j}} {||\vec{v_j}||^2}\right|\right)\mbox{sign}(\vec{v_i}\cdot \vec{v_j})\vec{v_j}$

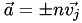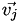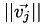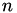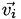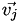This transformation adds a vector $\vec{a} = \pm n \vec{v_j}$ that is parallel to $\vec{v_j}$ with length that is an integer multiple of $||\vec{v_j}||$ . The multiplier $n$ is defined as the next highest integer from the absolute value of the scalar projection of $\vec{v_i}$ on $\vec{v_j}$ divided by the length of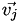 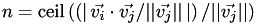$\vec{v_j}$ $n = \mbox{ceil}\left(\left(\left|\,\vec{v_i}\cdot \vec{v_j}/ ||\vec{v_j}||\,\right|\right)/||\vec{v_j}||\right)$ )}. The sign of 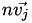$n\vec{v_j}$ from is determined by 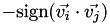$-\mbox{sign}(\vec{v_i}\cdot\vec{v_j})$ , resulting in the transformation equation above. For clarification, see the preceeding image.

These equations differ somewhat from those provided by Oganov et al., since the above equations apply to arbitrary length vectors, while those published for Oganov's USPEX code seem to only be applicable to unit vectors.

Atomic coordinates are stored in Cartesian form before the lattice transformation to maintain the structure's atomic configuration. After the new angles are set, the atoms are adjusted so that they lie within the new cell by adding or subtracting 1 from the new fractional coordinates.